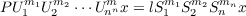|
Let S1,S2,⋯,,Sn be a set of
commuting contraction operators on a Hilbert space H, let U1,U2,⋯,Un be a set of
commuting unitary operators on a Hilbert space K containing H, and let P be the
projection from K to H. The set U1,⋯,Un is called a set of commuting unitary
dilations for S1,⋯,Sn provided that
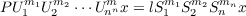
for all x in H and for all nonnegative integers m1,m2,⋯,mn. Sz.-Nagy proved that a
single contraction has a unitary dilation, and Ando showed that any two commuting
contractions possess a pair of commuting unitary dilations. This note presents several
counterexamples which disprove the corresponding conjecture for three or more
contractions.
In §3, three commuting contractions, R,S,T are constructed which do not have
commuting unitary dilations. The operators R and S each have norm one, while
the operator T may be chosen to have any norm between zero and one.
However, the proof yielding the counterexample fails completely if the operators
R,S,T are replaced by λR,λS,T with 0 < λ < 1, and this raises another
question.
It is known that a finite or infinite set of commuting contractions S1,S2,⋯ which
satisfies ∑
∥Sk∥2 ≦ 1 possesses a set of commuting unitary dilations. Thus it appears
that the “size” of a set of contractions may be relevant to the existence of commuting
unitary dilations; and since two of the contractions in §3 have norm one, it is
conceivable that this example might be only a peculiar “boundary” phenomenon. In
§4 this notion is dispelled by a more complicated example showing that three
commuting contractions, each of norm strictly less than one, can fail to have
commuting unitary dilations. Although the example of §4 is in most (but not all)
respects more powerful than that of §3, the latter is presented separately because of
its simplicity.
Section 3 also observes that a recent result of Sz.-Nagy and Foias is equivalent to
Ando’s theorem. Section 5 shows that the counterexamples constructed in this paper
to the unitary dilation conjecture cannot be used as counterexamples to another
well-known conjecture concerning spectral sets.
|