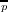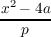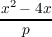Finite transformation formulae involving the Legendre symbol

Kenneth S. Williams

Vol. 34 (1970), No. 2, 559–568

DOI: 10.2140/pjm.1970.34.559

Abstract

Let p denote an odd prime. The following three identities (transformation formulae) involving the Legendre symbol () are known to be valid for any complex-valued function F defined on the integers, which is periodic with period p:

∑ x=0p−1F(x)	+ ∑ x=0p−1()F(x)		= ∑ x=0p−1F(x2),
∑ x=0p−1F(x)	+ ∑ x=0p−1()F(x)		= ∑ x=1p−1F(x + ),a≢0( mod p),
∑ x=0p−1F(x)	+ ∑ x=0p−1()F(x)		= ∑ x=1p−1F(x + 2 + ).

We consider a general class of transformation formulae, which includes the above examples.

Mathematical Subject Classification

Primary: 10.43

Milestones

Received: 26 August 1969

Revised: 30 January 1970

Published: 1 August 1970