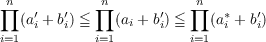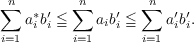Rearrangement inequalities involving convex functions

David London

Vol. 34 (1970), No. 3, 749–753

DOI: 10.2140/pjm.1970.34.749

Abstract

Let a = (a₁,⋯,a_n) and b = (b₁,⋯,b_n) be n-tuples of nonnegative numbers. Then

(1)

and

(2)

a′ = (a_i′,⋯,a_n′) and a^∗ = (a₁^∗,⋯,a_n^∗) are respectively the rearrangement of a in a nondecreasing or nonincreasing order. (1) was recently found by Minc and (2) is well known. In this note we show that these inequalities are special cases of rearrangement inequalities valid for functions having some convex properties.

Mathematical Subject Classification

Primary: 26.70

Milestones

Received: 26 February 1970

Published: 1 September 1970