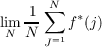|
The author constructs some
abstract algebras whose elements are subsets of the positive integers, and such that
the measure of a set is its density. These algebras 𝒜 are “abstract” in the sense that
the countable join in the underlying lattice is not ordinary set union. However they
are “concrete” in the sense that the elements of the algebra are sets, the
notion of an integrable function is available and the normed vector space of
integrable functions can be shown to be isometrically isomorphic to an ordinary
L1 space. If a function f is integrable, it is shown that its integral is given
by
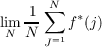
where f∗ is a suitably chosen function differing from f only on a set of density
0.
This construction differs from others (several are described by Kubilius in his
book on probabilistic methods in number theory), because usually countable
additivity is sacrificed, whereas here the meaning of countable join has been
altered.
|