|
This paper studies the
group G(A × B) of (homotopy classes of) self-homotopy equivalences of a
product A × B of two connected CW homotopy associative H-spaces A
and B. It establishes the existence of an exact sequence of multiplicative
groups
![1 → [A ∧ B,A × B ] → G (A × B ) → GL (2,ΛIJ) → 1](a170x.png)
provided that i∘ [A×B,A×B] ∘q ∘ [A∧B,A×B] = 0, where q : A×B → A∧B is
the cofibration induced by the inclusion i : A ∨ B → A × B of the sum into the
product. The entry GL(2,ΛIJ) is the group of invertible matrices
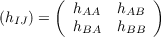
with entries hIJ in the homotopy sets ΛIJ = [I,J] for I,J = A,B, where matrix
multiplication is defined by
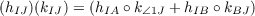
in terms of composition ∘ and the operation + in the homotopy sets [I,J], and
where the multiplicative unit is
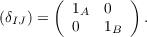
The homomorphism G(A × B) → GL(2,ΛIiI) is given by the correspondence of
h : A × B → A × B with the matrix
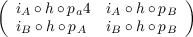
with entries obtained from h by composing with the inclusions iA : A → A×B and
iB : B → A × B and the projections pA : A × B → A and pB : A × B → B; for a
preliminary result states that under the hypothesis above h : A × B → A × B is a
homotopy equivalence if and only if the matrix (iI ∘ h ∘ pJ) is invertible.
A homotopy equivalence f ×g : A×B → A×B is referred to as untwisted. These
determine a subgroup G(A) × G(B) ⊂ G(A × B) which is isomorphic under the
homomorphism G(A×B) → GL(2,ΛIJ) to the subgroup of diagonal matrices, and so
the nondiagonal matrices give measure of the twisted selfhomotopy equivalences
A × B → A × B. The extreme case in which all self-homotopy equivalences are
untwisted is considered, and it is shown that G(A) ×G(B) = G(A×B) if and only if
the homotopy sets [A,B], [B,A], and [A ∧ B,A × B] are trivial.
Next, four settings are considered in which
![i∘[A × B,A × B]∘ q∘[A ∧ B,A × B] = 0](a175x.png)
and the exact sequence is valid. In the last section the dual situation of the group
G(M ∨N) of self-homotopy equivalences of a sum M ∨N of two co-H-spaces M and
N is briefly sketched.
|




![1 → [A ∧ B,A × B ] → G (A × B ) → GL (2,ΛIJ) → 1](a170x.png)
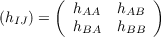
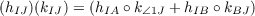
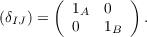
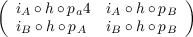
![i∘[A × B,A × B]∘ q∘[A ∧ B,A × B] = 0](a175x.png)

