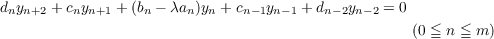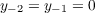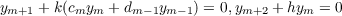|
We consider in this paper
boundary problems for the fiveterm scalar recurrence relation 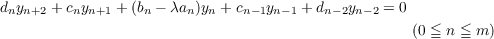 |
(1.1)
|
where the coefficients an,bn,cn,dn are real, an,dn > 0 and λ is a complex
parameter, with boundary conditions of the typical form
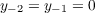 | (1.2) |
and
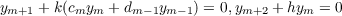 | (1.3) |
for some integer m ≧ 0, and real numbers h,k.
We derive oscillation properties, orthogonality relations and associated
eigenvector expansion theorems for solutions of (1.1), (1.2), (1.3), and then discuss
the solution of boundary problems for the corresponding inhomogeneous recurrence
relation in terms of a Green’s function.
|