Generalized Bol functional equation

Valentin Danilovich Belousov and Palaniappan L. Kannappan

Vol. 35 (1970), No. 2, 259–265

DOI: 10.2140/pjm.1970.35.259

Abstract

Each identity in a group or in a quasigroup induces a generalized identity (functional equation) in a class of quasigroups. Generalized associativity, generalized bisymmetry and generalized distributivity are examples of such generalized identities. From the left Bol identity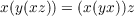

on a quasigroup, we obtain a generalized Bol identity on a class of quasigroups: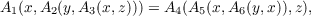

where the A_i’s are quasigroup operations on a set Q. The general solution of this generalized Bol functional equation is obtained by reducing it to another functional equation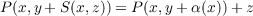

where P and S are quasigroup operations on Q and α(x) = S(x,0). If the operations in the last functional equation are considered on real numbers (or groups), then the solution of this equation is obtained.

Mathematical Subject Classification

Primary: 20.95

Milestones

Received: 5 February 1970

Published: 1 November 1970