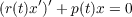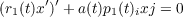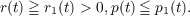Oscillation theorems for second order linear differential equations

Lynn Harry Erbe

Vol. 35 (1970), No. 2, 337–343

DOI: 10.2140/pjm.1970.35.337

Abstract

It is the purpose of this paper to show that oscillation of the linear second order equation

(1)

implies oscillation of the equation

(2)

for a large class of positive functions a(t), where the following condition holds for all large t:

(H)

We shall also assume that the functions r(t),r₁(t),p(t),p₁(t), and a(t) are continuous on some half line [T,+∞).

Mathematical Subject Classification

Primary: 34.42

Milestones

Received: 15 October 1969

Published: 1 November 1970