The derived set of the spectrum of a distribution function

Theodore Seio Chihara

Vol. 35 (1970), No. 3, 571–574

DOI: 10.2140/pjm.1970.35.571

Abstract

Let {a_n}_n=0^∞ and {b_n}_n=0^∞ be real sequences with b_n > 0, b_n → 0(n →∞). Let {P_n(αj)}_n=0^∞ be the sequence of orthonormal polynomials satisfying the recurrence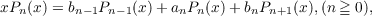

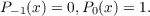Then there is a substantially unique distribution function ψ with respect to which the P_n(x) are orthogonal. This paper verifies a conjecture of D. P. Maki that the set of all limit points of the sequence {a_n} is the derived set of the spectrum of ψ.

Mathematical Subject Classification

Primary: 42.15

Milestones

Received: 9 March 1970

Published: 1 December 1970