Differential mappings on a vector space

Howard Barrow Lambert

Vol. 35 (1970), No. 3, 669–672

DOI: 10.2140/pjm.1970.35.669

Abstract

Let E and F be two normed vector spaces with real scalars, and G an open subset of E. A mapping f : E → F is said to be differentiable at x in G if there is a bounded linear map L : E → F such that for every y in G,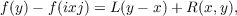

where R : E → F and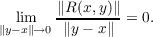

L is called the differential of f at x. An extension of this definition is possible is such a way as to include a point x on the boundary of G. In such cases f is said to have a differential at x from side G. Some properties of side differentials and relationships between the differential of f at x and its side differentials at x are shown in this paper. Theorems 1, 2, 3, and 4, listed below without proofs, are known theorems. The balance of the paper will be used to extend this theory.

Mathematical Subject Classification

Primary: 46.45

Milestones

Received: 10 December 1969

Published: 1 December 1970