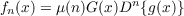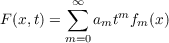A general theorem for bilinear generating functions

S. Saran

Vol. 35 (1970), No. 3, 783–786

DOI: 10.2140/pjm.1970.35.783

Abstract

The following theorem was proved by Chatterjea for ultraspherical polynomials:

then

where b_r(y) = ∑ _m=0^∞(v_m)a_my^m and ρ = (1 − 2xt + t²)^1∕2. The object of this paper is to show that a general theorem for any polynomial satisfying certain conditions can be given so as to include the above case, and may be applicable in obtaining new generating functions for other polynomials also.

Theorem. If

(1.1)

where g(x) and G(x) are independent of n, and

(1.2)

then

where

Mathematical Subject Classification

Primary: 33.20

Milestones

Received: 7 April 1970

Published: 1 December 1970