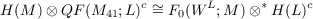The Frobenius reciprocity theorem and essentially bounded induced representations

William Louis Armacost

Vol. 36 (1971), No. 1, 31–43

DOI: 10.2140/pjm.1971.36.31

Abstract

Let G be a locally compact group with continuous unitary representations R_i acting on the Hilbert spaces H(R_t),i = 1,2. Suppose that R₂ is irreducible. A closed subspace of H(R₁), called the null space coming from R₁ at R₂ and denoted F(R₁;R₂), is defined. Write ℋ^c for the conjugate space of the Hilbert space ℋ. The following theorem is proved.

Theorem 1. Let G be a compact group with closed subgroup H. Let M,L be irreducible unitary representations of G,H, respectively. Let U^L be the induced representation of L, and let M_E be the restriction of M to H. Then the following are equivalent:

(a) The classical Frobenius Reciprocity Theorem.

(b) H(M) ⊗ F(M_II;L)^c≅F(U^L;M) ⊗ H(L)^c.

When G is not compact, both (a) and (b) may fail. A non-Hilbert Banach space induced representation (W^L) is defined. Let G be a locally compact group with closed subgroup H. Let M,L be irreducible unitary representations of G,H, respectively, where H(L) is separable. Spaces F₀(W^L;M) ⊗^∗H(L)^c (shown to equal F(U^L;M) ⊗ H(L)^c when G is compact) and QF(M_E;L) shown to equal F(M_H;L) when L is compact) are defined. The following generalization of (b) is shown.

Theorem 2. Let G,H,L be as above. Then

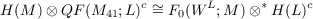
Mathematical Subject Classification

Primary: 22.60

Milestones

Received: 10 October 1969

Published: 1 January 1971