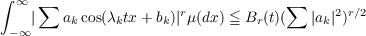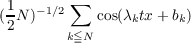|
In this note we continue some
investigations connecting a lacunary series Λ of real numbers
and a probability measure μ on (−∞,∞) satisfying
![μ([a,a + h]) ≪ hβ](a171x.png) | (1) |
for all intervals [a,a + h] of length h < 1, and a fixed exponent 0 < β < 1. (The
notation X ≪ Y is a substitute for X = 0(Y ).) Measures μ occur in the theory of
sets of fractional Hausdorff dimension.
In the following statements S is a subset of (−∞,∞) of Lebesgue measure 0,
depending only on μ and Λ.
Theorem 1. For r = 2,4,6,⋯ and t∉S, there is a constant Br(t) so that
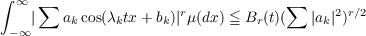
Here Br(t) is independent of the sequences (aj) and (bk).
Theorem 2. For t∉S the normalized sums
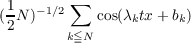
tend in law (with respect to the probability μ) to the normal law. Here the
convergence is uniform for all sequences (bk).
|
