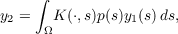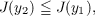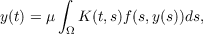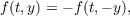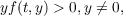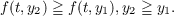|
Consider the linear integral
equation,
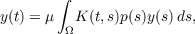 | (1) |
where K(s,t) is a real-valued symmetric positive definite kernel and p(s) is a positive
function. Let L denote the inverse of the integral operator u →∫
Ω K(⋅,s)u(s)ds, and
for a function y in the domain of L,y≠0, (all functions are assumed to be real valued)
define the Rayleigh quotient J(y) for (1) by,
dt∕ p(t)y2(t)dt.
Ω Ω](a041x.png)
If y1≠0 and y1 is in the domain of L and if
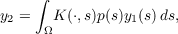
Shen several applications of the Schwarz inequality show that,
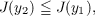
with equality only if y1 is an eigenfunction of (1). On the basis of this fact, when the
integral operator in (1) is compact, one can develop the complete spectral theory of
(1).
In this paper it is shown that the approach indicated above for the study of (1)
has a simple and natural extension for the study of the nonlinear integral
equation,
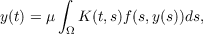 | (2) |
where K(t,s) is as above and f(t,y) is an odd function of y,
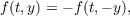
and satisfies,
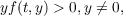
and
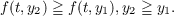
|





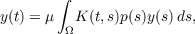
dt∕ p(t)y2(t)dt.
Ω Ω](a041x.png)