Volterra transformations of the Wiener measure on the space of continuous functions of two variables

W. N. Hudson

Vol. 36 (1971), No. 2, 335–349

DOI: 10.2140/pjm.1971.36.335

Abstract

The transformation of Wiener integrals over the space C₂ of continuous functions of two variables by a Volterra operator T is investigated. The operator T is defined for functions x ∈ C₂ by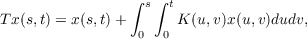

where the kernel K(u,v) is continuous. A stochastic integral analogous to K. Ito’s is defined and used to determine a Jacobian J(x) for T such that if F(x) is a Wiener measurable functional, Γ a Wiener measurable set, and m Wiener measure,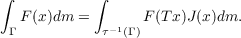

Mathematical Subject Classification

Primary: 28.46

Secondary: 60.00

Milestones

Received: 21 April 1970

Published: 1 February 1971