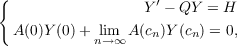Inverting operators for singular boundary value problems

Caulton Lee Irwin

Vol. 36 (1971), No. 2, 379–386

DOI: 10.2140/pjm.1971.36.379

Abstract

Let S denote a Banach Space, B the bounded linear transformations on S, and let Q and A denote functions from [0,∞) into B with Q continuous. The objective here is to derive a Green’s function K_A and hence an integral inverting operator R_A for the singular boundary value problem

(1)

where {c_n}_n=1^∞ is a positive, increasing, unbounded number sequence and H is a continuous function from [0,∞) into S.

Mathematical Subject Classification

Primary: 47.10

Secondary: 34.00

Milestones

Received: 11 February 1970

Published: 1 February 1971