|
In the course of an
investigation ofsix-dimensional complex linear groups, it was discovered that a central
extension of Z6 by PSU4(3) has a representation of degree six. In fact, this
representation has as its image the unimodular subgroup X(G) of index 2 of the
following 6-dimensional matrix group:  all 6 by 6 permutaion matrices; all
unimodular diagonal matrices of order 3; I6 − Q∕3 where Q has all its entries
equal to one all 6 by 6 permutaion matrices; all
unimodular diagonal matrices of order 3; I6 − Q∕3 where Q has all its entries
equal to one 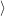 . This matrix group leaves the following lattice invariant: . This matrix group leaves the following lattice invariant:
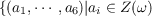 where throughout this paper ω is a primitive third root of
unity; ai − aj ∈ where throughout this paper ω is a primitive third root of
unity; ai − aj ∈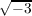 Z(ω) for all i,j; Z(ω) for all i,j; 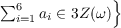 . The generators of the
matrix group are similar to the following generators for an 8-dimensional
complex linear group with Jordan-Holder constituents Z2, the nontrivial simple
constituent of 08(2),Z2; . The generators of the
matrix group are similar to the following generators for an 8-dimensional
complex linear group with Jordan-Holder constituents Z2, the nontrivial simple
constituent of 08(2),Z2;  all 8 by 8 permutation matrices, all unimodular
diagonal matrices of order 2, I8 − P∕4 where P has all entries equal to 1 all 8 by 8 permutation matrices, all unimodular
diagonal matrices of order 2, I8 − P∕4 where P has all entries equal to 1
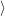 . .
The projective representation of PSU4(3) can be used to construct a
12-dimensional representation Y (H), a central extension of Z6 by the Suzuki group,
which leads to the known 24-dimensional projective representation of the Conway
group. In fact, H has a subgroup K isomorphic to a central extension of
(Z6 × Z3) by PSU4(3). Also, Y |H has two six-dimensional constituenls coming
from the above matrix group where the constiluents are related by an outer
automorphism of PSU4(3) which does not lift to the central extension of Z6 by
PSU4(3) with the six-dimensional representation. We obtain two commuting
automorphisms, α and β respectively, of G from I6 − Q∕3 and complex
conjugation. For PSU4(3), the outer automorphism group is dihedral of order eight
with its center corresponding to complex conjugation of X(G). The entire
automorphism group lifls to K. We may take the center of K to be ⟨a,b,c⟩
with a and b of order 3 and c of order 2, with G≅K∕b, and with α(a) = a,
α(b) = b−1, β(a) = a−1, β(b) = b−1. We can also find an automorphism γ of K
with γ(a) = b and γ(b) = a. We give the character table of K giving only
one representative of each family of algebraically conjugate characters and
classes. Irrational characters and classes are underlined. Only one class in each
coset of Z(K) is represented by the character tables. The characters in the
table U4(3) give the characters with Z(K) in the kernel. The succeeding five
character tables in order give the following linear characters, respectively, on
Z(K) : 𝜃(a) = 𝜃(b) = 1,0(c) = −1; 𝜃(a) = ω, 𝜃(b) = 𝜃(c) = 1; 𝜃(a) = ω−1,
𝜃(b) = 1, 𝜃(c) = −1; 𝜃(a) = 𝜃(b) = ω, 𝜃(c) = 1; 𝜃(a) = 𝜃(b) = ω, 𝜃(c) = −1. The
characters with other actions are obtained by applying elements of the outer
automorphism group. The automorphism α transposes π7 with π7−1; and N1
with N1−1 in the character tables. The automorphism β transposes N1
with N1−1; and N2 with N2−1. The automorphism γ transposes T1 with
T2; JT1 with JT2; N1 with N2; N1−1 with N2−1; and possibly π7 with
π7−1. As SU4(3)∕Ω(ZSU4(3)) has the centralizer of some central involution
isomorphic to the centralizer of some central involution J in G, presumably
SU4(3)∕Ω1(ZSU4(3))≅G∕03(Z(G)).
|





 all 6 by 6 permutaion matrices; all
unimodular diagonal matrices of order 3;
all 6 by 6 permutaion matrices; all
unimodular diagonal matrices of order 3; 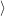 . This matrix group leaves the following lattice invariant:
. This matrix group leaves the following lattice invariant:
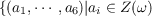 where throughout this paper
where throughout this paper 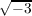
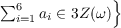 . The generators of the
matrix group are similar to the following generators for an 8-dimensional
complex linear group with Jordan-Holder constituents
. The generators of the
matrix group are similar to the following generators for an 8-dimensional
complex linear group with Jordan-Holder constituents  all 8 by 8 permutation matrices, all unimodular
diagonal matrices of order 2,
all 8 by 8 permutation matrices, all unimodular
diagonal matrices of order 2, 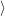 .
.
