On generalized translated quasi-Cesàro summability

B. T. Y. Kwee

Vol. 36 (1971), No. 3, 731–740

DOI: 10.2140/pjm.1971.36.731

Abstract

Let α > 0,β > −1. The (C_t,α,β) transformation of the sequence {s_k} is defined by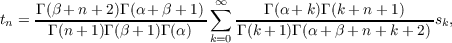

and the (C_t,α,β) transformation of the function s(x) is defined by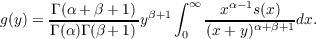

Some properties of the above two transformations are given in this paper and the relation between the summability methods defined by these transformations is discussed.

Mathematical Subject Classification 2000

Primary: 40G05

Milestones

Received: 1 December 1969

Published: 1 March 1971