Inversion of the Hankel potential transform

Frank Michael Cholewinski and Deborah Tepper Haimo

Vol. 37 (1971), No. 2, 319–330

DOI: 10.2140/pjm.1971.37.319

Abstract

We consider the Hankel potential transform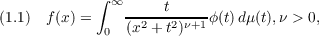

where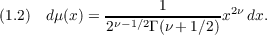

This transform is intimately related to the Hankel transform. Indeed, its kernel is the Hankel transform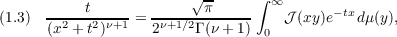

where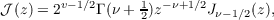

J_γ(z) being the ordinary Bessel function of order γ. Our object is to develop an inversion theory for (1.1) and to exploit the relationship of (1.1) to the Hankel transform.

Mathematical Subject Classification 2000

Primary: 44A15

Milestones

Received: 2 November 1970

Revised: 13 January 1971

Published: 1 May 1971