Universal coefficient theorems for generalized homology and stable cohomotopy

Paul C. Kainen

Vol. 37 (1971), No. 2, 397–407

DOI: 10.2140/pjm.1971.37.397

Abstract

We show that if h is a nice (e.g. representable) homology functor and G is an Abelian group, then there is a cohomology functor k(X;G) which is a “quasi-functor” of G and a short exact sequence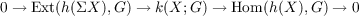

which is natural in X, “strongly quasi-natural” in G, and split if two additional conditions are satisfied.

Mathematical Subject Classification

Primary: 55J20

Milestones

Received: 23 October 1970

Revised: 24 February 1971

Published: 1 May 1971