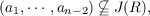|
In this paper, R always denotes
a commutative ring with identity. The ideal of nHpotents and the Jacobson radical of
the ring R are denoted by N(R) and J(R), respectively. The vector [a1,⋯,an] is
called a primitive row vector provided 1 ∈ (a1,⋯,an); a primitive row vector
[a1,⋯,an] is called completable provided there exists an n × n unimodular matrix
over R with first row a1,⋯,an. A ring R is called a B-ring if given a primitive row
vector [α1,⋯,an],n ≧ S, and
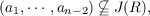
there exists b ∈ R such that 1 ∈ (a1,⋯,αn−2,an−1 + ban). Similarly, R is defined to
be a Strongly B-ring ( SB-ring), if d ∈ (a1,⋯,an),n ≧ 3, and (a1,⋯,an−2)⊈J(R)
implies that there exists b ∈ R such that d ∈ (a1,⋯,an−2,an−1 + ban).
In this paper it is proved that every primitive vector over a B-ring is completable.
It is shown that the following are B-rings: π-regular rings, quasi-semi-local rings,
Noetherian rings in which every (proper) prime ideal is maximal, and adequate rings.
In addition it is proved that R[X] is a B-ring if and only if R is a completely
primary ring. It is then shown that the following are SB-rings: quasi-local
rings, amy ring which is both an Hermite ring and a B-ring, and Dedekind
domains. Finally, it is shown that R[X] is an SB-ring if and only if R is a
field.
|