|
If a function x(σ),0 ≦ σ ≦ t, is
in Lip−α,0 < α < 1,x(0) = 0 and if ck(k = 0,1,2,⋯) are its Fourier coefficients with
respect to the functions 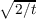 sin[π(k + sin[π(k + 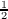 )σ∕t], then it is known [1, pp. 171–172]
that )σ∕t], then it is known [1, pp. 171–172]
that
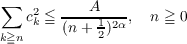 | (1) |
where A is a positive number not depending on n. We will show a connection
between this estimate and an estimate for Wiener integrals. Let Ew{ } denote
expectation on a Wiener process, that is, a Gaussian process with mean function
zero, covariance function min(σ,τ),0 ≦ σ,τ ≦ t and sample functions z(σ) with
z(0) = 0.
Theorem: Let x(σ) be in C[0,t] and let ck be the Fourier coefficients of x(σ) with
respect to the normalized eigenfunctions associated with min(σ,τ). That
is
![∘ --∫ t
ck = 2 x(σ )sin[π(k + 1)σ∕t]dσ.
t 0 2](a263x.png)
Let 0 < α < 1. Then estimate (1) is a necessary and sufficient condition for the
estimate
![∫
−(B ∕2)ν1−α EW {e−(ν∕2) 0t[z(σ)− x(σ)]2dσ}
e ≦ ---------−(ν∕2)∫t-2----------
EW {e 0 z (σ)dσ}](a264x.png) | (2) |
for all positive ν, where B is a positive number not depending on
ν.
|





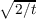
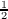
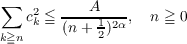
![∘ --∫ t
ck = 2 x(σ )sin[π(k + 1)σ∕t]dσ.
t 0 2](a263x.png)
![∫
−(B ∕2)ν1−α EW {e−(ν∕2) 0t[z(σ)− x(σ)]2dσ}
e ≦ ---------−(ν∕2)∫t-2----------
EW {e 0 z (σ)dσ}](a264x.png)
