|
|||||

|

|
|

|

|
|
Inequalities for
positive integral operators
David W. Boyd |
|
Vol. 38 (1971), No. 1, 9–24
|
Abstract |
|
The aim of this paper is to study integral inequalities of the following form, where T is an integral operator with nonnegative kernel: 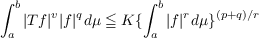 Classical examples of such inequalities include Hardy’s inequality and Opial’s inequality. Our main result (Theorem 1) is a minimax characterization of the best constants in such inequalities, under the condition that 1 ≦ p + q ≦ 7⋅. This theorem allows us to deduce certain facts concerning the uniqueness of the extremal functions. We then apply these results to the explicit computation or estimation of the best constants in inequalities of the form: 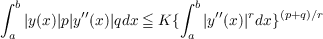 where y(α) = y(b) = 0. |
Mathematical Subject Classification
Primary: 26A84
|
Milestones
Received: 7 January 1971
Published: 1 July 1971
|
Authors |
| David W. Boyd | |
| Department of Mathematics University of British Columbia Vancouver BC V6T 1Z2 Canada |
|
| http://www.math.ubc.ca/~boyd/boyd.html | |
 |
