On the limiting distribution of additive functions (mod 1)

P. D. T. A. Elliott

Vol. 38 (1971), No. 1, 49–59

DOI: 10.2140/pjm.1971.38.49

Abstract

A function f(n), defined on the positive rational integers, is said to be additive if and only if for every pair of coprime integers a and b the relation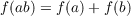

is satisfied. Thus an additive function is determined by its values on those integers which are prime powers. In an extensive paper Erdos raised the question of characterising those real valued additive functions which have a limiting distribution ( mod 1).

It is our present purpose to give such a characterisation.

Mathematical Subject Classification

Primary: 10K05

Milestones

Received: 11 May 1970

Published: 1 July 1971