A sufficient condition for L^p-multipliers

Satoru Igari and Shigehiko Kuratsubo

Vol. 38 (1971), No. 1, 85–88

DOI: 10.2140/pjm.1971.38.85

Abstract

Suppose 1 ≦ p ≦∞. For a bounded measurable function ϕ on the n-dimensional euclidean space Rⁿ define a transformation T_ϕ by (T_ϕf)^∧ = ϕf, where f ∈ L² ∩ L^p(Rⁿ) and f is the Fourier transform of f: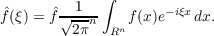

If T_ϕ is a bounded transform of L^p(Rⁿ) to L^p(Rⁿ), ϕ is said to be L^p-multiplier and the norm of ϕ is defined as the operator norm of T_ϕ.

Theorem 1. Let 2n∕(n + 1) < p < 2n∕(n− 1) and ϕ be a radial function on Rⁿ, so that, it does not depend on the arguments and may be denoted by ϕ(r),0 ≦ r < ∞. If ϕ(r) is absolutely continuous and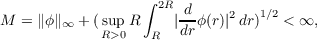

then ϕ is an L^p-multiplier and its norm is dominated by a constant multiple of M.

Mathematical Subject Classification

Primary: 42A18

Milestones

Received: 12 October 1970

Published: 1 July 1971