Examples concerning sum properties for metric-dependent dimension functions

John Charles Nichols and James C. Smith

Vol. 38 (1971), No. 1, 151–159

DOI: 10.2140/pjm.1971.38.151

Abstract

Let d₀ denote the metric dimension function defined by Katětov, and let dim be the covering dimension function. K. Nagami and J. H. Roberts introduced the metric-dependent dimension functions d₂ and d₃, and J. C. Smith defined the functions d₆ and d₇. The following relations hold for all metric spaces (X,ρ):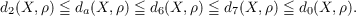

Since all of the metric-dependent dimension functions above satisfy a “Weak Sum Theorem,” it is natural to ask if any of these functions satisfy the Finite Sum Theorem or the Countable Sum Theorem. In this paper the authors obtain new properties of these dimension functions, and using these results construct examples for which none of the metric dependent dimension functions satisfy either of the sum theorems in question.

Mathematical Subject Classification 2000

Primary: 54F45

Milestones

Received: 2 March 1971

Published: 1 July 1971