Sharp estimates of convolution transforms in terms of decreasing functions

Gary Sampson

Vol. 38 (1971), No. 1, 213–231

DOI: 10.2140/pjm.1971.38.213

Abstract

Let f ∗g denote the convolution transform of two Lebesgue measurable functions on the real line defined by the equation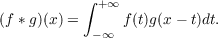

We get best possible upper and lower estimates for the expression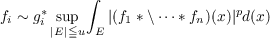

where p = 1 and 2, with applications to Fourier transform inequalities. Here g_λ^∗ are preassigned decreasing functions and the symbol f_i ∼ g_i^∗ means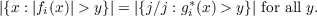

Mathematical Subject Classification 2000

Primary: 42A96

Secondary: 44A35

Milestones

Received: 18 November 1970

Published: 1 July 1971