|
This note presents a
generalization of Fatou’s lemma to arbitrary normed linear spaces. Several examples
illustrate the situations in which this notion is meaningful. The main theorem
gives an abstract characterization of the Fatou property. In particular this
resolves the case of any reflexive space. An example shows that Fatou’s lemma
may fail even for uniform convergence in a normed algebra of continuous
functions.
Frequently in analysis one obtains a function by a limiting process which is
weaker (less demanding) than convergence in the norm. For example, a continuous
function may be obtained as the point-wise, but not necessary uniform, limit of other
continuous functions. Even though the limit is not a norm limit, one may still need to
know that the norm of the limit function is no greater than the norms of the
approximating functions. The classical case is, of course, Fatou’s lemma: if fn → f
pointwise, then
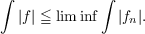
Another common situation is this. A subspace A ⊆ C(X) is given which has a
norm, ∥f∥≧ sup|f|. If fn → f pointwise (or uniformly), does it follow that
∥f∥≦ liminf ∥fn∥ ? The answer is “yes” quite often, but can be “no,” even when A is
a subalgebra.
|