|
|||||

|

|
|

|

|
|
Whittaker constants for
entire functions of several complex variables
Ken Shaw |
|
Vol. 38 (1971), No. 1, 239–250
|
Abstract |
|
Let f be an entire function of a single complex variable. The exponential type of f is given by 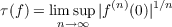 The Whittaker constant W is defined to be the supremum of numbers c having the following property: if τ(f) < c and each of f,f′,f′′,⋯ has a zero in the disc |z|≦ 1, then f ≡ 0. The Whittaker constant is known to lie between .7259 and.7378. The present paper provides a definition and characterization of the Whittaker constant 𝒲n for n complex variables. The principle result of this characterization, which involves polynomial expansions of entire functions, is 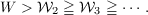 |
Mathematical Subject Classification 2000
Primary: 32A15
|
Milestones
Received: 30 October 1970
Published: 1 July 1971
|
Authors |
| Ken Shaw | |
 |
