Two uniform boundedness theorems

James DeWitt Stein

Vol. 38 (1971), No. 1, 251–260

DOI: 10.2140/pjm.1971.38.251

Abstract

A geodesically convex space is a metric space in which each two points can be connected by a unique segment (a path of minimal length). An affine transformation between two geodesically convex spaces is a map which takes segments into segments. It is shown that, if the domain is complete, a pointwise-bounded family of continuous affine transformations is uniformly bounded. Under a mild additional hypothesis, the following stronger theorem holds: if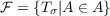

is a pointwise-bounded family of affine transformatons and T_a is continuous on a closed geodesically convex S_α with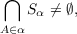

then ∃α₁,⋯,α_n such that 𝒯⁻ is uniformly bounded on

Mathematical Subject Classification 2000

Primary: 52A50

Secondary: 54H20

Milestones

Received: 17 March 1970

Revised: 14 April 1971

Published: 1 July 1971