A note on annihilator ideals of complex bordism classes

Larry Smith

Vol. 38 (1971), No. 2, 551–558

DOI: 10.2140/pjm.1971.38.551

Abstract

Recent studies of the complex bordism homology theory Ω_∗^U() have shown that for a finite complex X the integer hom-dim 0_⋆^UΩ_∗^U(X) provides a useful numerical invariant measuring certain types of complexity in X. Associated to an element α ∈ Ω_∗^U(X) one has the annihilator ideal A(α) ⊂ Ω_∗^U. Numerous relations between A(α) and hom-dim l2_∼^UΩ_∗^U(X) are known. In attempting to deal with these invariants it is of course useful to study special cases, and families of special cases. In this note we study the annihilator ideal of the canonical element σ ∈∼^NU9Ω(X) where X is a complex of the form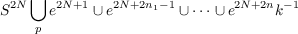

and N >> n₁,⋯n_k > 1, and p an odd prime. We show that A(σ) a [V ^2p2−2 ],⋯,[V ^2pS−2 ],⋯⋅, where [V ^2pS−2 ] ∈ Ω_2p^S−2^U is a Milnor manifold for the prime p. This provides another piece of evidence that for such a complex X, hom-dim Ω_∗^UΩ_∗^U(X) islor2.

Mathematical Subject Classification

Primary: 57C20

Secondary: 57D99

Milestones

Received: 5 February 1971

Published: 1 August 1971