|
|||||

|

|
|

|

|
|
Directed graphs as
unions of partial orders
Peter C. Fishburn and Joel Spencer |
|
Vol. 39 (1971), No. 1, 149–161
|
Abstract |
|
The index of an irreflexive binary relation R is the smallest cardinal number σ(R) such that R equals the union of σ(R) partial orders. With s(n) the largest index for an R defined on n points, it is shown that s(n)∕log 2n → 1 as n →∞. The index function is examined for symmetric R’s and almost transitive R′s, and a characterization for σ(R) ≦ 2 is presented. It is shown also that 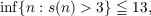 but the exact value of inf{n : s(n) > 3} is presently unknown. |
Mathematical Subject Classification 2000
Primary: 05C20
|
Milestones
Received: 22 July 1970
Revised: 12 October 1970
Published: 1 October 1971
|
Authors |
| Peter C. Fishburn | |
| Joel Spencer | |
| New York University NY United States |
|
 |
