On the solution of linear G.C.D. equations

David Jacobson and Kenneth S. Williams

Vol. 39 (1971), No. 1, 187–206

DOI: 10.2140/pjm.1971.39.187

Abstract

Let Z denote the domain of ordinary integers and let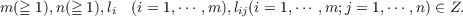

We consider the solutions x ∈ Zⁿ of G.C.D.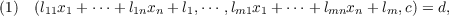

where c(≠0),d(≧ 1) ∈ Z and G.C.D. denotes “greatest common divisor”. Necessary and sufficient conditions for solvability are proved. An integer t is called a solution modulus if whenever x is a solution of (1), x + tg is also a solution of (1) for all y ∈ Zⁿ. The positive generator of the ideal in Z of all such solution moduli is called the minimum modulus of (1). This minimum modulus is calculated and the number of solutions modulo it is derived.

Mathematical Subject Classification

Primary: 10C99

Milestones

Received: 30 November 1970

Revised: 1 April 1971

Published: 1 October 1971