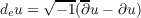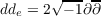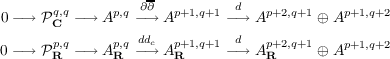Cohomology groups associated with the ∂∂operator

Let M be a complex analytic manifold of complex dimension m. The manifold M, considered open, is a submanifold of a manifold M′ of the same dimension, and its boundary ∂M is a smooth C⁸-manifold. Let A^p,q be the sheaf of germs of complex-valued (p,q)-forms, p and q are integers, p ≧ 0,q ≧ 0. The exterior differential of an element u ∈ A^p.q can be written in a unique way as a sum du = ∂u + ∂u. There is a real operator

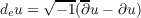
deu = √ − 1(∂u − ∂u)

and the real second order operator

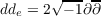
√--- -- dde = 2 − 1∂∂

defined on Apq. Let A_R^p,q = {α = α₁ + α₂ ∈ A^p.q ⊕ A^q,p|α₂ = α₁} be the sheaf of real (p,q)-forms. Then we get two short exact sequences of sheaves

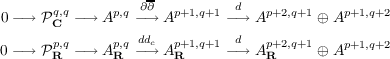∂∂ d 0 −→ 𝒫q,Cq− → Ap,q−→ Ap+1,q+1 −→ Ap+2,q+1 ⊕ Ap+1,q+2 p,q p,q ddc p+1,q+1 d p+2,q+1 0 −→ 𝒫 R − → A R −→ AR −→ A R ⊕ Ap+1,q+2

(1.1)

where 𝒫_c^p,q and 𝒫_R^p,q are defined by these sequences. The purpose of this paper is to discuss the cohomology of these two sequences.

Mathematical Subject Classification 2000

Primary: 32C35

Secondary: 58G05

Milestones

Received: 3 August 1970

Published: 1 November 1971

Authors

Bohumil Cenkl


Giuliano Sorani

Vol. 39, No. 2, 1971

Bohumil Cenkl and Giuliano Sorani

Abstract

Mathematical Subject Classification 2000

Milestones

Authors