Summability and Fourier analysis

George Ulrich Brauer

Vol. 40 (1972), No. 1, 33–43

DOI: 10.2140/pjm.1972.40.33

Abstract

An integration on βN, the Stone-Cech compactification of the natural numbers N, is defined such that if s is a bounded sequence and ϕ is a summation method evaluating s to σ, ∫ sdϕ = σ. The Fourier transform ϕ of a summation method ϕ is defined as a linear functional on a space of test functions analytic in the unit disc: if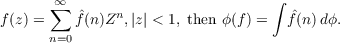

A functional which agrees with the Fourier transform of a regular summation method must annihilate the Hardy space H₁. Our space of test functions is often the space M,, of functions f = ∑ f(n)zⁿ, analytic in the unit disc, such that

is finite for some p > 1. A functional L which is well defined on a space M_p for some p ≧ 2 such that L(1∕(1 − z)) = 1 agrees with the Fourier transform of a summation method which is slightly stronger than convergence.

Mathematical Subject Classification 2000

Primary: 42A68

Secondary: 40H05, 30A78

Milestones

Received: 6 August 1970

Published: 1 January 1972