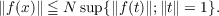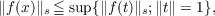|
Let F be a family of functions
on subsets of a real Euclidean space E into a commutative subalgebra with identity
T0 of the algebra T of linear transformations of E into itself. If a suitable integration
condition, motivated by Morera’s theorem in complex function theory is placed on
the elements of F,F becomes an algebra of “integrable” functions which can be
realized as the derivatives of transformations of E into itself. It is asked what
properties of the algebra of complex analytic functions from the complex
plane K into K are satisfied by such algebras F. Simple examples show that
analyticity and even differentiability are lost. However various forms of the
maximum modulus theorem are still satisfied. Three such theorems are presented
here:
(A) If commutivity of T0 is replaced by the requirement that the elements of T0
are “orientation preserving” then the elements of F are maximized on the boundary
of a sphere.
(B) There exists N > 0, such that for all f ∈ F, U = {t ∈ E;∥t∥≦ 1}⊆ domain
f,x ∈U , implies
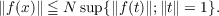
(C) For all f ∈ F,U ⊆ domain f,x ∈U, implies
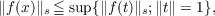
where for A ∈ T0,∥A∥s is the spectral norm of A.
|