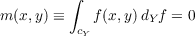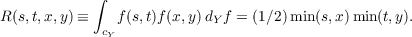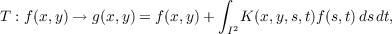On Fredholm transformations in Yeh-Wiener space

Let C_Y denote the Yeh-Wiener space, i.e., the space of all real-valued continuous functions f(x,y) on I² ≡ [0,1] × [0,1] such that f(0,y) = f(x,0) ≡ 0. Yeh has defined a Gaussian probability measure on C_Y such that the mean of the process

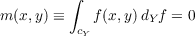
∫ m (x,y) ≡ f(x,y)d f = 0 cY Y

and the convariance

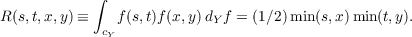
∫ R(s,t,x,y) ≡ f (s,t)f (x,y)dY f = (1∕2)min(s,x)min(t,y). cY

Consider now a linear transformation of C_Y onto C₁ of the form

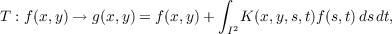∫ T : f(x,y) → g(x,y) = f (x,y)+ 2K (x,y,s,t)f (s,t)dsdt, I

(1.1)

which is often called a Fredholm transformation. The main purpose of this paper is to find the corresponding RadonNikodym derivative thus showing how the Yeh-Wiener integrals transform under the transformation.

Mathematical Subject Classification

Primary: 28A40

Milestones

Received: 23 October 1970

Published: 1 January 1972

Authors

Chull Park

Vol. 40, No. 1, 1972

Chull Park

Abstract

Mathematical Subject Classification

Milestones

Authors