A three point condition for surfaces of constant mean curvature

Eamon Boyd Barrett

Vol. 40 (1972), No. 2, 269–277

DOI: 10.2140/pjm.1972.40.269

Abstract

Let ϕ(x,y) be a solution to the equation: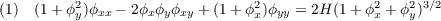

The quantity H in equation (1) represents the mean curvature of the surface z = ϕ(x,y). In case H = 0, (1) is the minimal surface equation. For minimal surfaces, the wellknown three point condition may be stated as follows:

Theorem 1. Let ϕ(x,y) be a solution to the Dirichlet problem for the minimal surface equation in some bounded region R. Let T be the continuous space curve defined by the values of ϕ(x,y) over ∂R, the boundary of R. Then, if P is a plane tangent to the surface z = ϕ(x,y) for (x,y) in R,P will have at least 4 points in common with T.

The objective of this paper is to establish a natural analogue of the three-point condition for surfaces of positive, constant mean curvature.

Mathematical Subject Classification 2000

Primary: 53A10

Milestones

Received: 23 November 1970

Published: 1 February 1972