Matrix inequalities and kernels of linear transformations

Peter Botta

Vol. 40 (1972), No. 2, 285–289

DOI: 10.2140/pjm.1972.40.285

Abstract

Let V be a finite dimensional unitary space and ⊗^mV the unitary space of m-contravariant tensors based on V with the inner product induced from V . If T is a linear transformation on ⊗^mV to itself and X = (αj_i,x_j) any positive semidefinite hermitian matrix define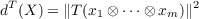

Let ∥ ∥₁ be any norm on the space of m × m complex matrices, and 𝒯 = {x₁ ⊗⋯ ⊗ x_m : x_i ∈ V }. The main result is that if T and S are any two linear transformations on ⊗ⁿV to itself then the following are equivalent:

(a) ker(T) ∩𝒯 ⊆ ker(S) ∩𝒯

(b) If X is positive semidefinite hermitian and d^T(X) = 0 then d^s(X) = 0.

(c) There exists a positive integer k and a constant c > 0 such that for all positive semidefinite hermitian matrices X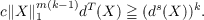

Some applications to inequalities for generalized matrix functions are given.

Mathematical Subject Classification 2000

Primary: 15A45

Milestones

Received: 10 November 1970

Published: 1 February 1972