On the operator M(Y ) = TY S⁻¹ in locally convex algebras

Florian Vasilescu

Vol. 40 (1972), No. 2, 489–500

DOI: 10.2140/pjm.1972.40.489

Abstract

Let U be a locally convex separated unitary algebra over the complex field. If T and S are fixed elements of A and S is invertible, it is possible to define on A the linear operator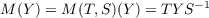

for all Y ∈ A. The purpose of this paper is to construct a functional calculus with analytic functions for the operator M(T,S), by means of T and S, in order to obtain “multiplicative variants” of some results of M. Rosenblum. In the last section these results are applied to normal operators and matrices.

Mathematical Subject Classification 2000

Primary: 46H05

Secondary: 47A60

Milestones

Received: 11 May 1970

Published: 1 February 1972