Exponential sums over GF(2ⁿ)

Kenneth S. Williams

Vol. 40 (1972), No. 2, 511–519

DOI: 10.2140/pjm.1972.40.511

Abstract

Let F = GF(q) denote the finite field with q = 2ⁿ elements. For f(X) ∈ F[X] we let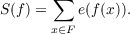

A deep result of Carlitz and Uchiyama states that if f(X)≠g(X)²+g(X)+b,g(X) ∈ F[X],b ∈ F, then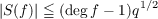

This estimate is proved in an elementary way when deg f = 3,4,5 or 6. In certain cases the estimate is improved.

Mathematical Subject Classification

Primary: 12C25

Milestones

Received: 6 August 1970

Published: 1 February 1972