|
|||||

|

|
|

|

|
|
Maximinimax, minimax,
and antiminimax theorems and a result of R. C. James
Stephen Simons |
|
Vol. 40 (1972), No. 3, 709–718
|
Abstract |
|
This paper contains a number of minimax theorems in various topological and non-topological situations. Probably the most interesting is the following: if X is a nonempty bounded convex subset of a real Hausdorff locally convex space E with dual E′ and each φ ∈ E′ attains its supremum on X then 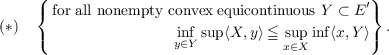 It is also proved that if (∗) is true and X is complete then X is w(E,E′)-compact. Combining these results, a proof of a well known result of R. C. James is obtained. |
Mathematical Subject Classification
Primary: 46A05
|
Milestones
Received: 28 January 1971
Published: 1 March 1972
|
Authors |
| Stephen Simons | |
 |
