On the asymptotic behavior of solutions of x′′ + a(t)f(x) = e(t)

Theodore Allen Burton and Ronald Calvin Grimmer

Vol. 41 (1972), No. 1, 43–55

DOI: 10.2140/pjm.1972.41.43

Abstract

In this paper sufficient conditions are given which insure that all solutions of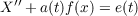

tend to zero as t →∞. Results obtained are comparable to those obtained for the linear equations via two Liouville transformations. Also, related results concerning stability and boundedness of solutions and, when e(t) = 0, necessary and sufficient conditions for the uniqueness of the zero solution on an interval where a(t) is negative are given.

Mathematical Subject Classification 2000

Primary: 34D05

Milestones

Received: 30 April 1971

Published: 1 April 1972