Group representations and the Adams spectral sequence

R. James Milgram

Vol. 41 (1972), No. 1, 157–182

DOI: 10.2140/pjm.1972.41.157

Abstract

Homotopy groups admit primary operations analogous to the Steenrod operations in ordinary cohomology theory and a good understanding of them seems vital to interpreting patterns in the homotopy of spheres.

Also, it has been known for a long time that a type of Steenrod algebra acts in Ext_A(Z_p,Z_p) if A is a cocommutative Hopf algebra. Recently, D. S. Kahn showed that in the E₂ term of the Adams spectral sequence Ext_𝒜(2)^∗∗(Z₂,Z₂), certain of these operations on infinite cycles converge to the graded elements associated to the actual homotopy operations. Also, on infinite cycles, he showed how this structure determined some differentials.

In this paper, we further explore the relations between the operations in Ext_𝒜(p)^∗∗(Z_p,Z_p) and differentials in the Adams spectral sequence. In particular, for elements which need not be infinite cycles, we prove

Theorem 4.1.1.

(a) There are operations Sqⁱ in Ext_𝒜(2)(Z₂,Z₂) so that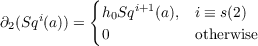

for a ∈ Ext_𝒜(2)^r,s(Z₂,Z₂).

(b) There are operations 𝒫ⁱ,β𝒫ⁱ in Ext_𝒜(p)(Z_p,Z_p) for p an odd prime so that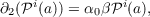

for a ∈ Ext_𝒜(p)^r,s(Z_p,Z_p). (Here, Sqⁱ takes Ext^s,r homomorphically to Ext^s+i,2r while 𝒫i takes Ext^s,r to Ext^{s+(2i−r)(p−1),pr}, and β𝒫ⁱ(Ext^s,r) ⊂ Ext^{s+(2i−r)(p−1)+1,pr}.)

Mathematical Subject Classification 2000

Primary: 18H10

Secondary: 20G99, 55H15

Milestones

Received: 19 October 1970

Published: 1 April 1972