Vector space decompositions and the abstract imitation problem

George Gustave Weill

Vol. 41 (1972), No. 1, 263–273

DOI: 10.2140/pjm.1972.41.263

Abstract

Let 𝒮 be a Hilbert space, 𝒫 a closed subspace of 𝒮L an orthogonal projection operator on 𝒮 The “imitation problem” consists of finding the solutions p ∈𝒫 of the equation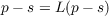

for given s ∈𝒮 If W is a compact bordered Riemann surface, A a boundary neighborhood, s a “singularity differential” defined on A,p will be a harmonic exact differential which imitates s on A in a sense precised by L (hence the name “imitation problem”). Existence and uniqueness theorems are given for the solution. Some concrete applications are described. The paper ends with a constructive method of solution in the case of L²-normal operators.

Mathematical Subject Classification

Primary: 46C10

Secondary: 30A48

Milestones

Received: 30 June 1970

Revised: 14 January 1971

Published: 1 April 1972