Differentiable power-associative groupoids

John P. Holmes

Vol. 41 (1972), No. 2, 391–394

DOI: 10.2140/pjm.1972.41.391

Abstract

Suppose H is a Banach space, D is an open set of H containing 0, and V is a function from D ×D to H satisfying V (0,x) = V (x,0) = x for each x in D. If n is an integer greater than 1, denote by xⁿ the product of n − x’s associated as follows whenever the product exists.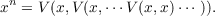

Define x⁰ = 0 and x¹ = x.V is said to be power associative if and only if V (xⁿ,x^m) = x^n+m whenever each of n and m is a nonnegative integer and x^n+m exists.

Theorem A. If H and V are as above, V is power associative and continuously differentiable in the sense of Frechet on D × D then there are positive numbers a and c such that if x is in H and ∥x∥ < a there is a unique continuous function T_x from [0,1] to the ball of radius c centered at 0 satisfying V (T_x(s),T_x(t)) = T_x(s + t) whenever each of s,t, and s + t is in [0,1],T_x(0) = 0, and T_x(1) = x.

Mathematical Subject Classification 2000

Primary: 46N05

Secondary: 20N99

Milestones

Received: 9 August 1971

Revised: 20 December 1971

Published: 1 May 1972