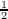|
Let W(t,ω) be the
Wiener process on an abstract Wiener space (i,H,B) corresponding to the
canonical normal distributions on H. Stochastic integrals ∫
0tξ(s,ω)dW(s,ω) and
∫
0t(ζ(s,ω), dW(s,ω)) are defined for non-anticipating transformations ξ with
values in ℬ(B,B) such that (ξ(i,ω) − I)(B) ⊂ B∗ and ζ with values in H.
Suppose X(t,ω) = x0+ ∫
0tξ(s,ω)dW(s,ω) + ∫
0tσ(s,ω)ds, where σ is a
non-anticipating transformation with values in H. Let f(t,x) be a continuous
function on R × B, continuously twice differentiable in the H-directions with
D2f(t,x) ∈ℬ1(H,H) for the x variable and once differentiable for the t variable. Then
f(t,X(t,ω)) = f(0,x0) + ∫
0tξ∗(s,ω)Df(s,X(s,ω))dW(s,ω) + ∫
0t{∂f∕∂s(s,X(s,ω)) +
⟨Df(s,X(s,ω)),σ(s,ω)⟩ + 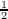 trace[ξ∗(s,ω)D2f(s,X(s,ω))ξ(s,ω)]}ds, where ⟨,⟩ is the
inner product of H. Under certain assumptions on A and σ it is shown that the
stochastic integral equation X(t,ω) = x0 + ∫
0tA(X(s,ω))dW(s,ω) + ∫
0tσ(X(s,ω))ds
has a unique solution. This solution is a homogeneous strong Markov
process.
|
