On the zeros of a polynomial and its derivative

Qazi Ibadur Rahman

Vol. 41 (1972), No. 2, 525–528

DOI: 10.2140/pjm.1972.41.525

Abstract

Let all the zeros of a polynomial p(z) of degree n lie in |z|≦ 1. Given a complex number a what is the radius of the smallest disk centred at α containing at least one zero of the polynomial ((z − a)p(z))^f? According to Theorem 1 the answer is (|a| + 1)∕(n + 1) if |α| > (n + 2)∕n. Theorem 2 which states that if both the zeros of the quadratic polynomial p(z) lie in |z|≦ 1 and |a|≦ 2 then ((z − α)p(z))′ has at least one zero in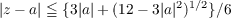

completely settles the case n = 2.

Mathematical Subject Classification

Primary: 30A08

Milestones

Received: 28 January 1971

Published: 1 May 1972