|
The locally equiconnected
spaces (LEC spaces) can be characterized as the spaces X with the property that if
f0,f1 : Z → X are mappings which are “sufficiently close together” and which agree
on a subspace A of Z, then f0 is homotopic to f1 relative to A(f0≅f1 rel A); i.e.,
there is a morphism F : Z × I → X with F|Z × 0 = f0,F|Z × 1 = f1 and
F(a,t) = f0a for all a ∈ A and t ∈ I.
The notion of “close” is measured by a morphism φ : X ×X → I with φ(x,x′) = 0
if and only if x = x′. We then require that φ(f0ξ,f1ξ) < 1 for all ξ ∈ Z implies that
f0≅f1 rel A.
There is a universal test pair (u,D); let u = φ−1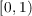 and D = φ−10. Let f0 and
f1 be the restrictions to u of the projections X × X → X onto the first
and second coordinates. Then f0 and f1 agree precisely on D. A homotopy
f0≅f1 relD exists if and only if D is a strong deformation retract of u in
X × X. and D = φ−10. Let f0 and
f1 be the restrictions to u of the projections X × X → X onto the first
and second coordinates. Then f0 and f1 agree precisely on D. A homotopy
f0≅f1 relD exists if and only if D is a strong deformation retract of u in
X × X.
We note two things. First, the existence of a homotopy f0≅f1 rel D implies the
existence of the homotopies in the general case described in the first paragraph.
Second, the existence of a map φ and homotopy f0≅f1 rel D is equivalent to the
diagonal map
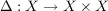
being a cofbration.
|




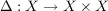

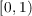 and
and 