Shock sets for first order nonlinear hyperbolic equations

Donald Pollard Ballou

Vol. 42 (1972), No. 1, 17–26

DOI: 10.2140/pjm.1972.42.17

Abstract

This paper studies those values u which can be reached from u₀ across a shock or contact discontinuity which may arise in weak solutions to the Cauchy problem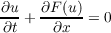

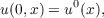where it is not assumed that F′′ > 0. A condition which guarantees uniqueness is used to define a set lS(u₀) consisting of such values u. The close relationship between lS(u₀) and the geometry of F(u) is examined, and properties of this set are derived which give information about the interaction of curves of discontinuity.

Mathematical Subject Classification 2000

Primary: 35L65

Milestones

Received: 2 March 1971

Published: 1 July 1972